The Einstein biographer Andrew Robinson, author of Einstein: A Hundred Years of Relativity , recently reminded me of the saga of Einstein’s blackboard. The blackboard, a well-known exhibit at the Oxford Museum for the History of Science, was used by Einstein in the second of three lectures he gave at Oxford University in 1931.
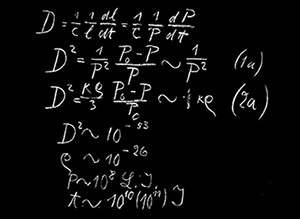
An image of the blackboard used in Einstein’s 2nd Rhodes lecture at Oxford in April 1931 (reproduced by permission of the Hebrew University of Jerusalem). The analysis is taken from Einstein’s 1931 model of the cosmos.
I came across Einstein’s blackboard during the course of our first Einstein study, a translation and analysis of Einstein’s 1931 paper on cosmology. Although the paper is not very well known in the English-speaking world, it is a work of historical importance, as it constituted the first scientific publication in which Einstein formally rejected his static model of the universe and embraced the possibility of a cosmos of time-varying radius. In the paper, Einstein adopts Alexander Friedman’s 1922 analysis of relativistic cosmic models of time-varying radius and positive curvature, but sets the cosmological constant to zero, predicting a cosmos that expands and contracts over time (the model is sometimes known as the Friedman-Einstein model and should not be confused with the later Einstein-deSitter model of the cosmos). With the use of Edwin Hubble’s redshift/distance graph for the spiral nebulae, Einstein extracts estimates from his analysis of ρ ~ 10-26 g/cm3 , P ~ 108 light-years and t ~ 1010 years for the density of matter, the radius of the cosmos and the timespan of the cosmic expansion respectively. However, our analysis of the paper indicated that Einstein’s estimates contain a systematic numerical error.
Before submitting our paper on this to a journal, I discovered to my great surprise that Einstein’s 1931 paper is neatly summarized on the Oxford blackboard (see above). Although the blackboard is quite well known as an intriguing museum exhibit, it seems no-one had made the connection with a published paper. Even better, one extra line on the blackboard, not included in Einstein’s published paper, makes clear the source of the numerical errors in the paper.
The analysis is quite easy to follow: for a cosmos of radius P, the quantity D is defined on the top line of the blackboard as D= (1/c). (1/P).(dP/dt): essentially the Hubble constant divided by the speed of light. From his earlier analysis, Einstein has developed two independent relations from the Friedman equations that relate D to the radius and density of the cosmos respectively: D2 ~ 1/P2 and D2 ~ 1/3 kρ, shown as equations (1a) and (2a) on the blackboard. Using the contemporaneous Hubble constant of 500 kms-1Mpc-1, he thus extracts estimates of cosmic density, radius and timespan of expansion respectively, displayed in the last three lines on the blackboard. However, these estimates contain errors as noted above, and the fourth line on the blackboard (not shown in Einstein’s published paper), makes the source of his error clear. Where Einstein obtains a value of 10-53 cm-2 for the quantity D2, simple calculation shows that this quantity should have been D2 ~ 10-55 cm-2 (or 10 -51 m-2). It appears that Einstein stumbled in converting the Hubble constant to his customary cgs units, resulting in a density of matter that was too high by a factor of a hundred, a cosmic radius that was too low by a factor of ten, and a timespan for the expansion that was too high by a factor of ten (although the units of measurement are not specifically stated for the density estimate, cgs units are implied by the other calculations).
Thus Einstein’s blackboard helped us to solve the riddle of the anomalous estimates of his 1931 paper! Our paper on this made the cover of the European Physical Journal and you can read more about Einstein’s blackboard on this blog here and on wikipedia here.
Update
All of the above was interesting and good fun. However, I should say that our translation and analysis of Einstein’s 1931 paper yielded another, rather more serious result – namely that the 1931 paper is NOT a cyclic model, although it is often cited as the first cyclic model of the expanding universe. Einstein specifically rules out this possibility, pointing out that the model breaks down at the endpoints of the single ‘cycle’.

Bravo, Cormac!
A beautiful piece of intellectual work, having both scientific and historical import. Have the curators of Oxford University’s exhibits been made aware of the significance of the fourth line of notation on the “Einstein blackboard”?
I think it fair to say that what you have successfully undertaken here is an example of what Alfred North Whitehead called an “Adventure of the Mind”.
Incidentally, I have come across assertions in a few biographies of Einstein to the effect that the Permanent Faculty of The Institute for Advanced Study at Princeton saw to it that the blackboard in Einstein’s office was preserved in the state in which it was found on the day in April, 1955 when he died. I wonder whether, assuming that this story is true, a similarly informed examination of that artefact might yield some likewise interesting insight.
Once again, nice job.
—Howard P. Kenig
Hey – what a great addition to a really great piece of investigation…. and a great blog post to boot.
Congratulations and Merry Christmas
Cormac
Thanks guys! I did in fact inform the Oxford museum of our finding, about two years ago now. The only action they took was to remove the existing label of the exhibit (which stated that the equations had never been published). However, last month Andrew Robinson gave a talk on Einstein’s time in Oxford during which he referred to our work; hopefully that will spur some action on the topic.